Az Enigma rejtélyének megfejtése, és a Turing-teszt megalkotása után Alan Turing új kihívásokat keresett és azokat végül a biológiában találta meg. Egész pontosan a biológiai minták matematikai leírása és képződésük feltételezett mechanizmusa kezdte izgatni zseniális elméjét és ennek a nyomát őrzi legendás 1952-es cikke, amelyben (egyebek mellett) megalkotta a foltszerű mintázatok leírására és modellezésére mindmáig leginkább használt "reakció-diffúzió mechanizmust".
Az Enigma rejtélyének megfejtése, és a Turing-teszt megalkotása után Alan Turing új kihívásokat keresett és azokat végül a biológiában találta meg. Egész pontosan a biológiai minták matematikai leírása és képződésük feltételezett mechanizmusa kezdte izgatni zseniális elméjét és ennek a nyomát őrzi legendás 1952-es cikke, amelyben (egyebek mellett) megalkotta a foltszerű mintázatok leírására és modellezésére mindmáig leginkább használt "reakció-diffúzió mechanizmust".
Turing zsenialtása már rögtön ott tettenérhető, hogy ráérzett, a látszólag random vonalak és foltok összessége jól megfogalmazható matematikai törvényszerűségeknek engedelmeskedik, amelyeknél elég néhány paraméter megváltoztatása és egészen különböző mintázatok leírását érhetjük el segítségükkel.
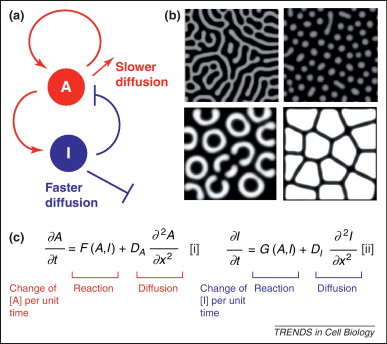 A szabály lényege, hogy ha van egy A aktivátor molekulám, ami pl. pigmentkialakulást okoz (de kültakarón kívül, mindez igaz minde más, molekuláris szinten detektálható mintára). Az A rendelkezik egy adott diffúziós konstanssal, meg persze azzal a tulajdonsággal, hogy aktiválja önmagát és I-t is, saját inhibitorát, jellgezetes pozitív illetve negatív feed-back köröket hozva létre. I szintén rendelkezik egy diffúziós konstanssal, ami történetesen nagyobb, mint az A megfelelő értéke. Ha mindez megvan, akkor minden adott a gyönyörű mintázatok kialakulásához.
A szabály lényege, hogy ha van egy A aktivátor molekulám, ami pl. pigmentkialakulást okoz (de kültakarón kívül, mindez igaz minde más, molekuláris szinten detektálható mintára). Az A rendelkezik egy adott diffúziós konstanssal, meg persze azzal a tulajdonsággal, hogy aktiválja önmagát és I-t is, saját inhibitorát, jellgezetes pozitív illetve negatív feed-back köröket hozva létre. I szintén rendelkezik egy diffúziós konstanssal, ami történetesen nagyobb, mint az A megfelelő értéke. Ha mindez megvan, akkor minden adott a gyönyörű mintázatok kialakulásához.
(A mellékelt ábra képletei ne ijesszenek meg senkit, tényleg nagyon könnyen megemészthetők. F(A,I) és G(A,I) a két molekula közti kölcsönhatást írja le, ami A szemszögéből nézve gátlás, I esetében pedig aktiválás, a DA és DI a két diffúziós konstans.)
A kiindulási állapot általában csak stochasztikus különbségeket rejt az aktivátor koncentrációjában, de ezek elegendők lesznek, hogy a pozitív feed-back segítségével az aktivátor ezeken a helyeken feldúsuljon. Ugyanakkor az inhibitor megjelenése és gyors diffúziója biztosítja, hogy ezek a feldúsulások csak lokálisak maradjanak és ne az egész szövet ússzon az aktivátorban. (Az alábbi ábrán A-ból P, I-ből pedig S lett, de egyébként minden ua..)
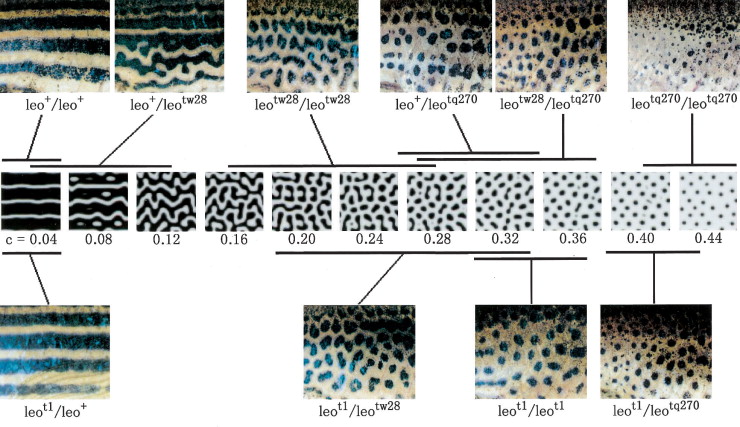
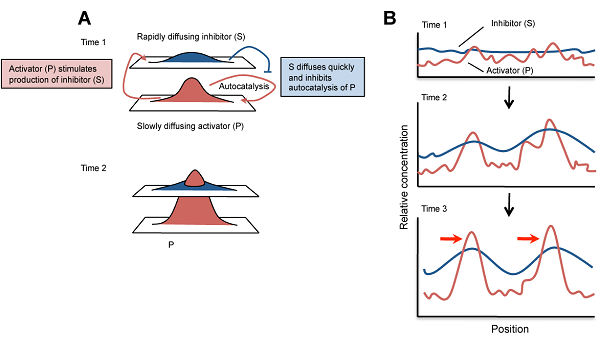 Ennyi a lényeg, a kezdeti paraméterek beállítása aztán majd ontja a minta-kavalkádokat. És ami még jobb: minden jel arra mutat, hogy ezek nagyon is jó leírói lesznek a valóságnak. Az alábbi ábrán egy pigmentáció mutáns zebradánió törzs (leopard) különböző erősségű mutáns alléjainak hordozóit láthatjuk összevetve egy szimulált mintasorozattal, ahol az aktivátor alap-szintétisének szintje - ezt fejezi ki a c - változik csak.
Ennyi a lényeg, a kezdeti paraméterek beállítása aztán majd ontja a minta-kavalkádokat. És ami még jobb: minden jel arra mutat, hogy ezek nagyon is jó leírói lesznek a valóságnak. Az alábbi ábrán egy pigmentáció mutáns zebradánió törzs (leopard) különböző erősségű mutáns alléjainak hordozóit láthatjuk összevetve egy szimulált mintasorozattal, ahol az aktivátor alap-szintétisének szintje - ezt fejezi ki a c - változik csak.
Persze nem a kültakaró mintája az egyetlen példa: a főbb jelátviteli útvonalak - Wnt, Nodal - egyaránt ezt a logikát használják önszabályozásra, ahogy még néhány más fejlődésbiológiai folyamat működése is ebbe az irányba mutat, de ezekről majd később.
Még több matematika a fejlődésbiológiában.
(A fiatal császárhal képe innen származik. Enigma rajongóknak pedig ez kötelező darab.)
A.M. Turing (1952) The chemical basis of morphogenesis. Phil. Trans. R. Soc., B237: 37–72.
Torii KU (2012) Two-dimensional spatial patterning in developmental systems. Trends in Cell Bio 22(8): 438–446.
Asai R, Taguchi E, Kume Y, Saito M, Kondo S (1999) Zebrafish leopard gene as a component of the putative reaction-diffusion system. Mech Dev 89(1-2): 87-92.